728x90
반응형
SMALL
회귀(Regression)란?
: 머신러닝과 통계학에서 연속적인 수치 값을 예측하거나 변수 간의 관계를 모델링하기 위한 분석 기법이다.
입력 변수(독립 변수, feature)가 출력 변수(종속 변수, target)에 어떻게 영향을 미치는지를 수학적 방식으로 모델링한다.
결정 트리 회귀(Decision Tree Regression)란?
: 결정 트리(Decision Tree)를 사용하여 연속적인 값(숫자 값)을 예측하는 회귀 방법이다.
데이터가 여러 구간으로 나뉘고, 각 구간에서 평균값이나 특정 기준을 사용하여 출력 값을 예측한다.

1) 두 클래스 분류의 불순물을 정의하는 방법
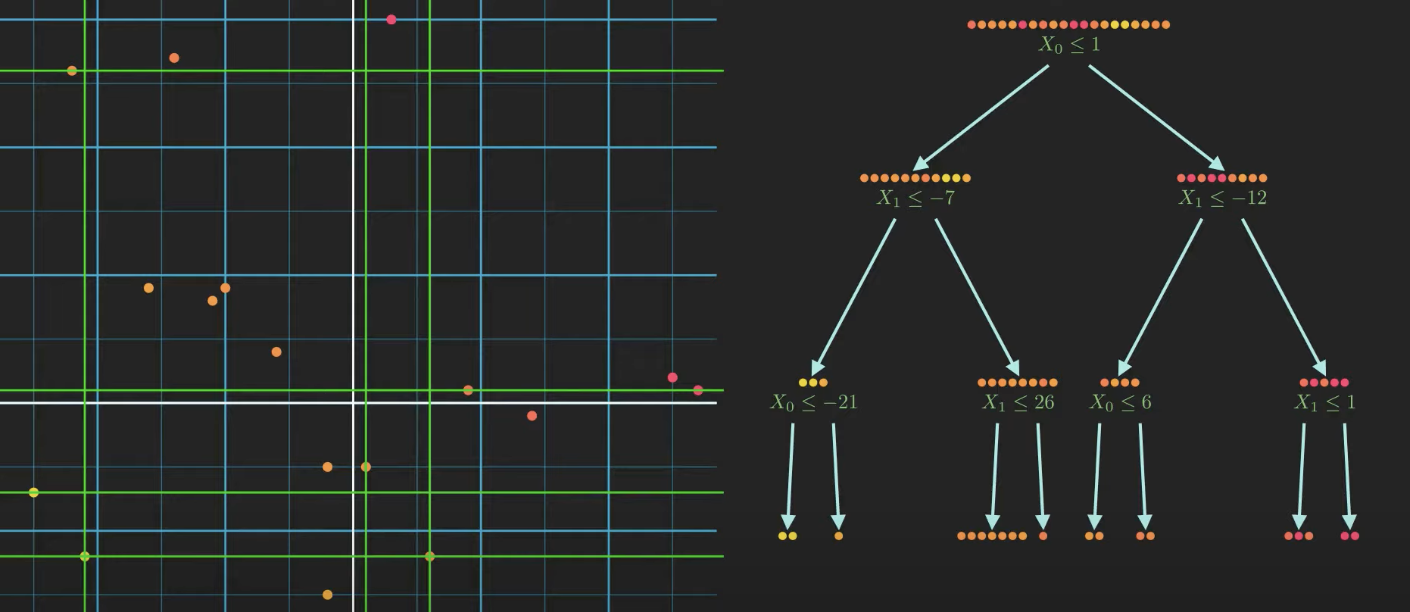
가능한 모든 분할에 대한 분산 감소를 평가하고 최상의 분할을 선택해야 함.
결정트리로 데이터를 조건에 따라 두 개의 하위집합으로 나눈 후, 하위노드의 데이터분산을 계산하여 이 분할이 유의미한지 평가한다.
- 트리는 재귀적으로 분할을 수행하며, 각 단계에서 가장 효과적인 조건(최대 분산 감소)을 찾는다.
- 분할 조건이 추가될수록 하위 노드의 분산은 감소하고, 데이터 포인트가 더욱 동질적인 그룹으로 나뉜다.
- 최종적으로 모든 데이터가 리프 노드에 도달하면, 각 리프 노드는 자신이 포함한 데이터 포인트의 평균 yy-값을 출력한다.
- 결정 트리 분할의 핵심은 데이터의 불순도(impurity)를 최소화하는 것이다.
- 회귀 트리에서는 분산을 사용하여 불순도를 측정한다
2) 예측하는 방법
- 데이터가 트리의 리프 노드(끝 노드)에 도달하면, 해당 노드에서 예측값을 생성한다.
- 예측값은 분류와 회귀에 따라 다른다.
분류 문제 (Classification):
- 리프 노드의 다수결을 사용하여 예측.
- 리프 노드에 포함된 데이터 포인트 중 가장 많은 클래스가 예측값이 된다.
회귀 문제 (Regression):
- 리프 노드의 평균값을 사용하여 예측합니다.
- 리프 노드에 포함된 데이터 포인트의 yy-값의 평균이 예측값이 됩니다.
- 예: 리프 노드에 yy-값이 5, 7, 9가 있다면 예측값은 (5+7+9) / 3 = 7 이
정리 !
1. 분할 기준을 설정하는 과정 (분할 기준 정의)
결정 트리는 데이터를 반복적으로 분할하여 예측력을 높이는 방식으로 작동한다.
1-1. 불순도 측정 (Impurity Measure)
- 데이터를 분할할 때, "불순도"를 최소화하는 방향으로 나누는 것이 목표.
- 불순도란 : 데이터 집합 내 클래스 또는 값의 혼란 정도를 나타냄.
- 불순도를 측정하는 주요 방법:
- 분류(Classification):
- 엔트로피 (Entropy): 데이터의 혼란도를 계산. 값이 클수록 데이터가 고르게 섞여 있음.
- 지니 지수 (Gini Index): 클래스 간의 불균형 정도를 측정.
- 회귀(Regression):
- 분산 (Variance): 연속형 데이터의 값들이 얼마나 퍼져 있는지를 계산.
- 분류(Classification):
1-2. 정보 이득 (Information Gain)
- 정보 이득은 불순도가 얼마나 감소했는지를 측정하는 값.
- 공식: Information Gain = 불순도(부모 노드)−(왼쪽 자식 불순도 × wl + 오른쪽 자식 불순도 × wr)
- wl, wr : 왼쪽/오른쪽 자식 노드의 가중치 (해당 노드의 데이터 비율).
1-3. 최적의 분할 기준 선택
- 모든 속성(feature)와 그 속성의 값(threshold)을 기준으로 데이터셋을 나눠보고, 정보 이득이 가장 높은 기준을 선택한다.
- 최적의 기준은 불순도를 최대한 줄이는 방향으로 결정된다.
2. 트리 구조의 생성 과정
2-1. 노드 생성
- 트리의 각 노드는 특정 속성(feature)을 기준으로 데이터를 분할한다.
- 각 노드는 다음과 같은 정보를 포함:
- 속성(feature): 데이터를 분할한 기준 속성.
- 임계값(threshold): 속성의 값을 기준으로 분할.
- 왼쪽/오른쪽 자식 노드: 분할된 데이터 집합.
2-2. 분할 반복 (재귀적 분할)
- 데이터를 반복적으로 분할하며 트리를 확장한다.
- 각 분할 후, 다시 자식 노드에서 최적의 분할 기준을 찾는다.
- 분할은 다음 조건에서 멈춥니다:
- 노드의 데이터가 동질적일 때 (한 클래스만 포함).
- 사전에 설정된 최대 깊이 (max depth)에 도달했을 때.
- 노드의 데이터 개수가 최소 분할 샘플 수 (min_samples_split)보다 작을 때.
3. 리프 노드에서 예측 수행
리프 노드는 트리의 끝에서 더 이상 분할되지 않는 노드입니다. 여기서 예측값을 생성한다.
3-1. 분류(Classification)
- 리프 노드의 다수결에 따라 클래스를 예측.
- 예: 리프 노드에 데이터가 클래스 A 7개, 클래스 B 3개라면 예측값은 클래스 A.
3-2. 회귀(Regression)
- 리프 노드의 데이터 값 평균을 예측값으로 사용.
- 예: 리프 노드의 값이 10, 12, 14라면 예측값은 (10+12+14) / 3=12.
결론: 결정 트리의 주요 목표
- 데이터를 반복적으로 분할하여 불순도를 최소화하고, 최적의 예측 규칙을 찾기
- 각 노드에서는 최적의 분할 기준을 정의하고, 자식 노드로 재귀적으로 확장하기
- 최종적으로 리프 노드에서 예측값을 계산하여 결과를 제공하기
https://colab.research.google.com/drive/1ljgZv39r0bzLWAHXVPuo1o2tDl4GH7oP?usp=sharing
Decision Tree Regression in Python
Colab notebook
colab.research.google.com
728x90
반응형
LIST
'💻 본업(컴공생) 이야기 > 머신러닝 - 딥러닝 이야기' 카테고리의 다른 글
| [CNN 공부하기] AlexNet, VGGNet, ResNet 은 뭘까? (2) | 2025.02.11 |
|---|---|
| [랩_스터디 과제 3] Gradient descent (경사하강법), how neural networks learn? 🧠 (2) | 2025.01.21 |
| [랩_스터디 과제 3] Deep learning (introduction) (2) | 2025.01.21 |
| [랩_스터디 과제 2] 발표준비 (0) | 2025.01.11 |
| [랩_스터디 과제 2] Decision Tree Classification (2) | 2025.01.11 |